Throughout the engineering, physical and biological sciences, many systems are known to have prescribed relationships between time and space that drive patterns of dynamical activity. Even simple spatio-temporal relationships can lead to highly complex, yet coherent, dynamics that motivate the main thrust of analytic and computational studies. Modeling efforts seek to derive these spatio-temporal relationships either through first principle laws or through well-reasoned conjectures about existing relationships, thus leading generally to an underlying partial differential equation (PDE) that constrains and governs the complex system. Reduced order models (ROMs) aim to exploit underlying, low-dimensional patterns of activity in order to promote improved understanding of the systems as well as computational efficiency.
Supplementary Videos

This video highlights some the basic structure of of the POD method applied to PDEs [ view ]
This video highlights the POD method as an optimal basis [ view ]
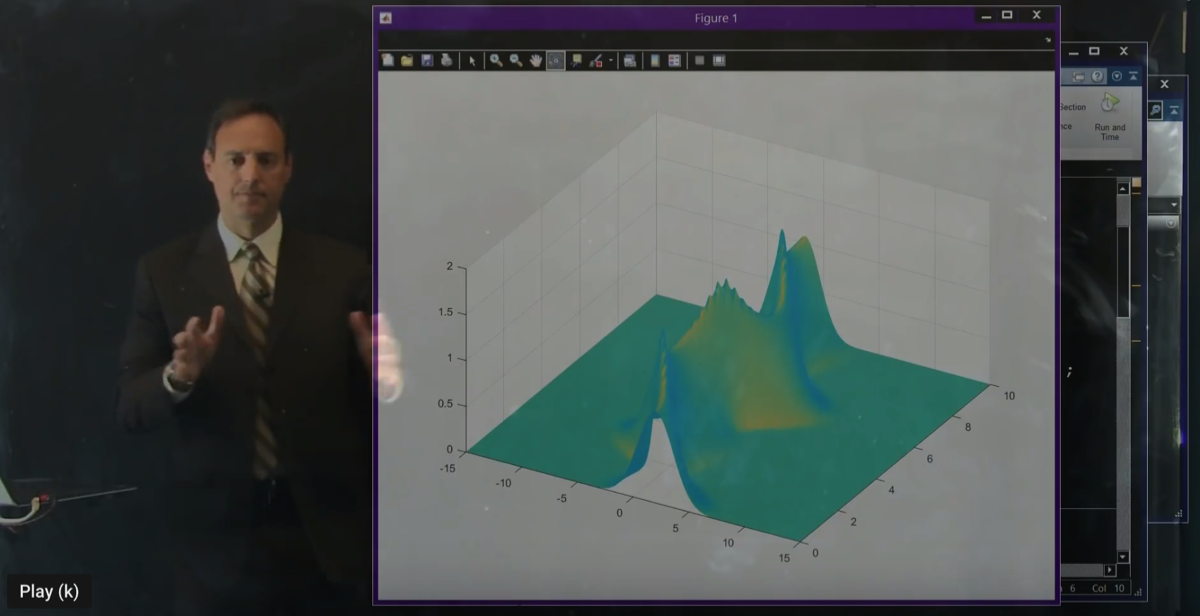
This video implements a Galerkin POD method on the nonlinear Schrödinger equation
[view ]
[view ]