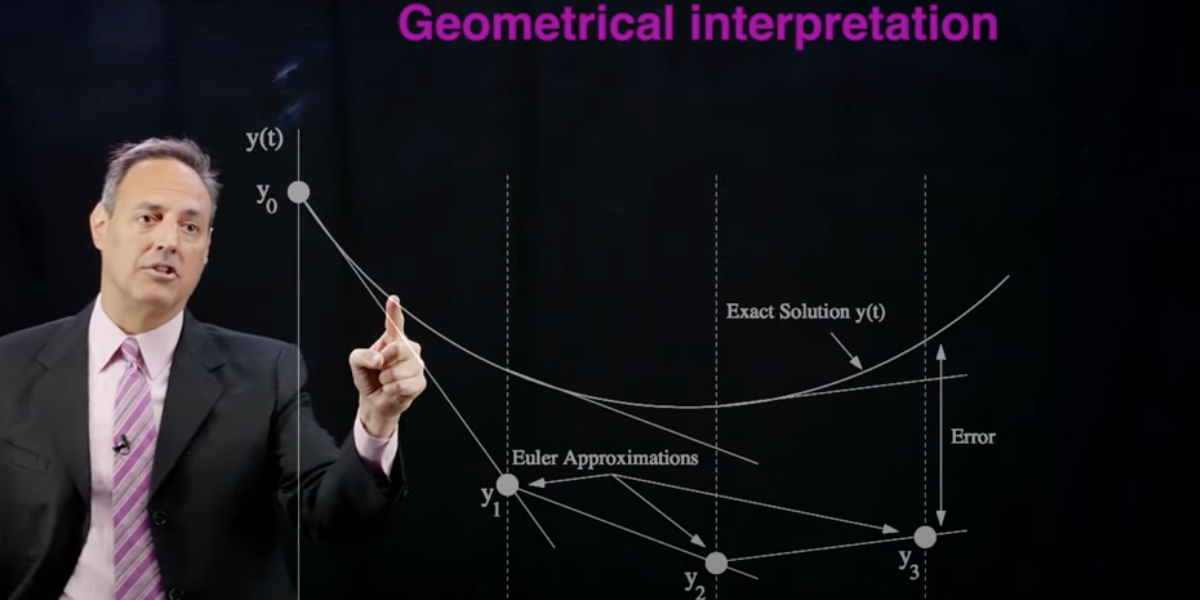
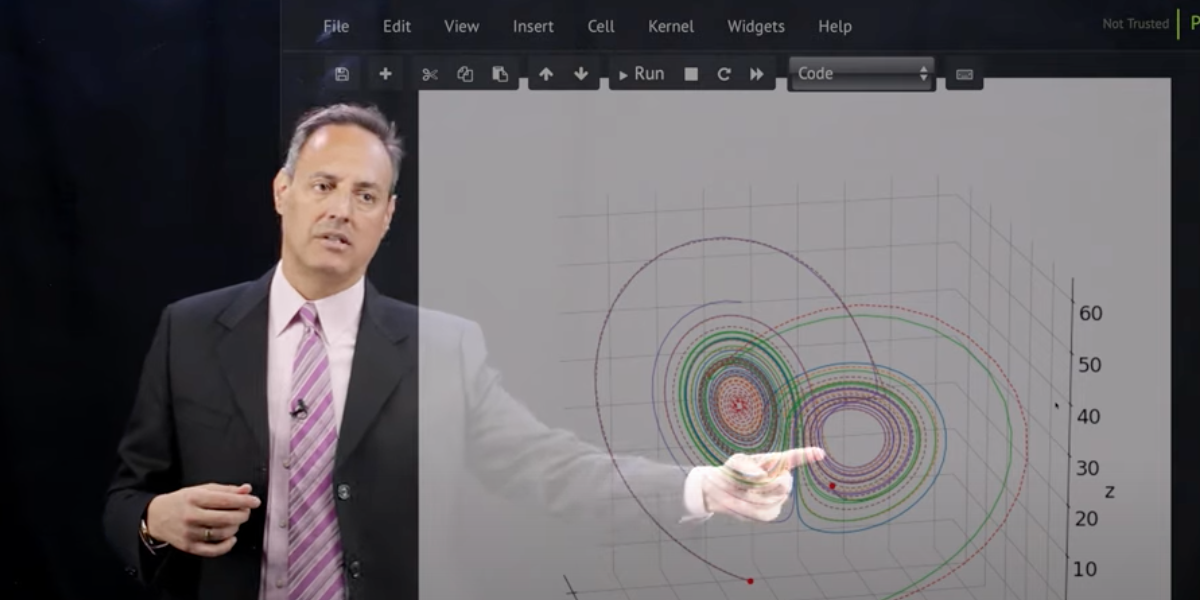
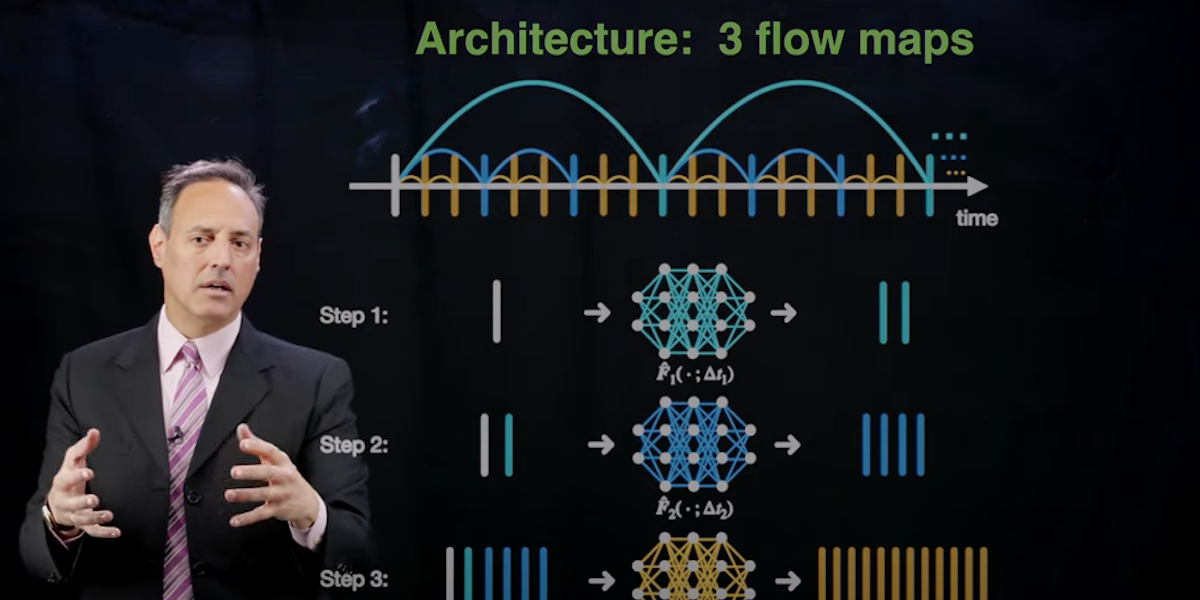
Time-stepping algorithms are critical for modeling systems that evolve in time. Fluid flows are typically spatio-temporal systems whose temporal evolution is dominated by nonlinear processes. In these lectures, we use neural networks to construct flow maps that characterise the evolution dynamics over a prescribed time increment. We further connect flow maps to standard numerical solvers such as Euler and Runge-Kutta steppers.
Key references
- Liu, Kutz & Brunton, Hierarchical Deep Learning of Multiscale Differential Equation Time-Steppers (2020)
- Gonzales, Rico-Martinez & Kevrekidis, Identification of distributed parameters systems: A neural net based approach (1998)
- Qin, Wu & Xiu, Data driven governing equations approximation using deep neural networks (2019)
- Parish & Carlberg, Time-series machine-learning error models for approximate solutions to parameterized dynamical systems (2020)
- Regazzoni, Dede & Quarteroni, Machine learning for fast and reliable solution of time-dependent differential equations (2019)
Jupyter notebook
- Time-stepping for Lorenz equation: lorenz_timestep.ipynb
Supplementary Videos
This video details the hierarchical time-stepping algorithm learned by neural networks [ VIEW ]