Chapter 1: Singular Value Decomposition | DATA DRIVEN SCIENCE & ENGINEERING

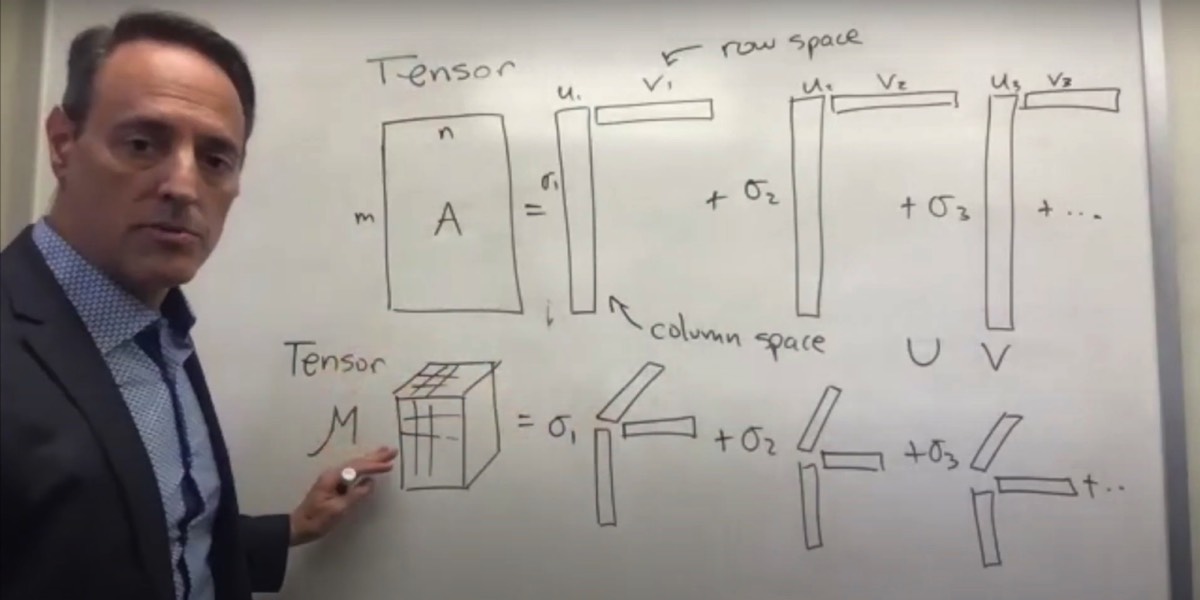
The singular value decomposition (SVD) is among the most important matrix factorizations of the computational era, providing a foundation for nearly all of the data methods in this book. We will use the SVD to obtain low-rank approximations to matrices and to perform pseudo-inverses of non-square matrices to find the solution of a system of equations. Another important use of the SVD is as the underlying algorithm of principal component analysis (PCA), where high-dimensional data is decomposed into its most statistically descriptive factors. SVD/PCA has been applied to a wide variety of problems in science and engineering.

In many domains, complex systems will generate data that is naturally arranged in large matrices, or more generally in arrays. For example, a time-series of data from an experiment or a simulation may be arranged in a matrix with each column containing all of the measurements at a given time. If the data at each instant in time is multi-dimensional, as in a high-resolution simulation of the weather in three spatial dimensions, it is possible to reshape or flatten this data into a high-dimensional column vector, forming the columns of a large matrix. Similarly, the pixel values in a grayscale image may be stored in a matrix, or these images may be reshaped into large column vectors in a matrix to represent the frames of a movie. Remarkably, the data generated by these systems are typically low rank, meaning that there are a few dominant patterns that explain the high-dimensional data. The SVD is a numerically robust and efficient method of extracting these patterns from data.

Youtube playlist: Singular Value Decomposition