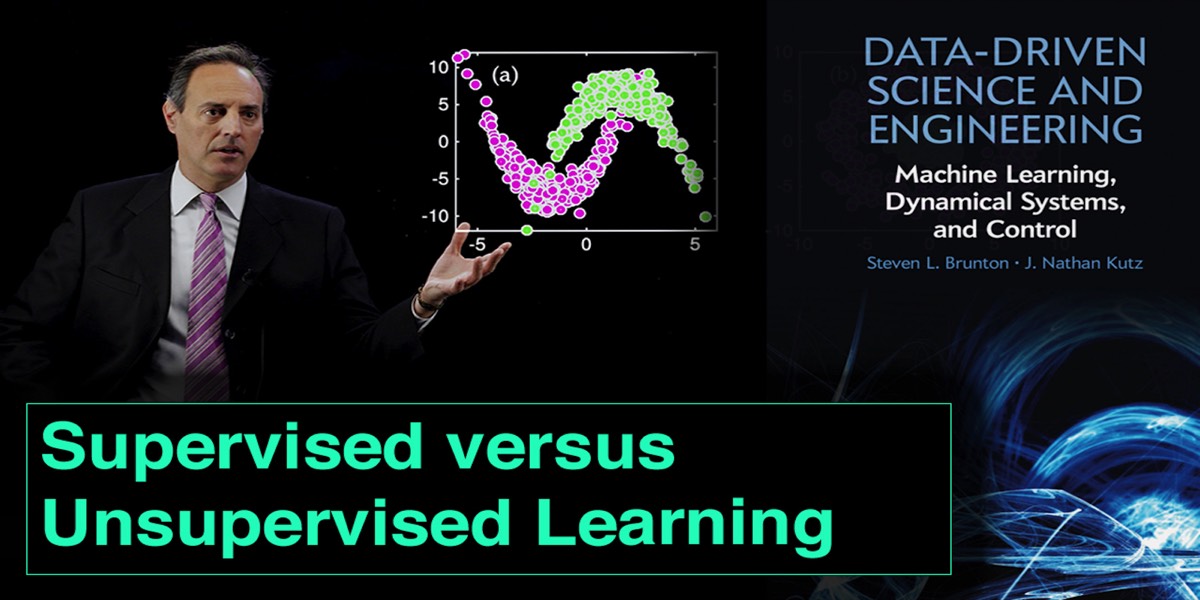
To exploit data for diagnostics, prediction and control, dominant features of the data must be extracted. In the opening chapter of this book, SVD and PCA were introduced as methods for determining the dominant correlated structures contained within a data set. In the eigenfaces example of Sec. 1.6, for instance, the dominant features of a large number of cropped face images were shown. These eigenfaces, which are ordered by their ability to account for commonality (correlation) across the data base of faces was guaranteed to give the best set of r features for reconstructing a given face in an l2 sense with a rank-r truncation. The eigenface modes gave clear and interpretable features for identifying faces, including highlighting the eyes, nose and mouth regions as might be expected. Importantly, instead of working with the high-dimensional measurement space, the feature space allows one to consider a significantly reduced subspace where diagnostics can be performed.
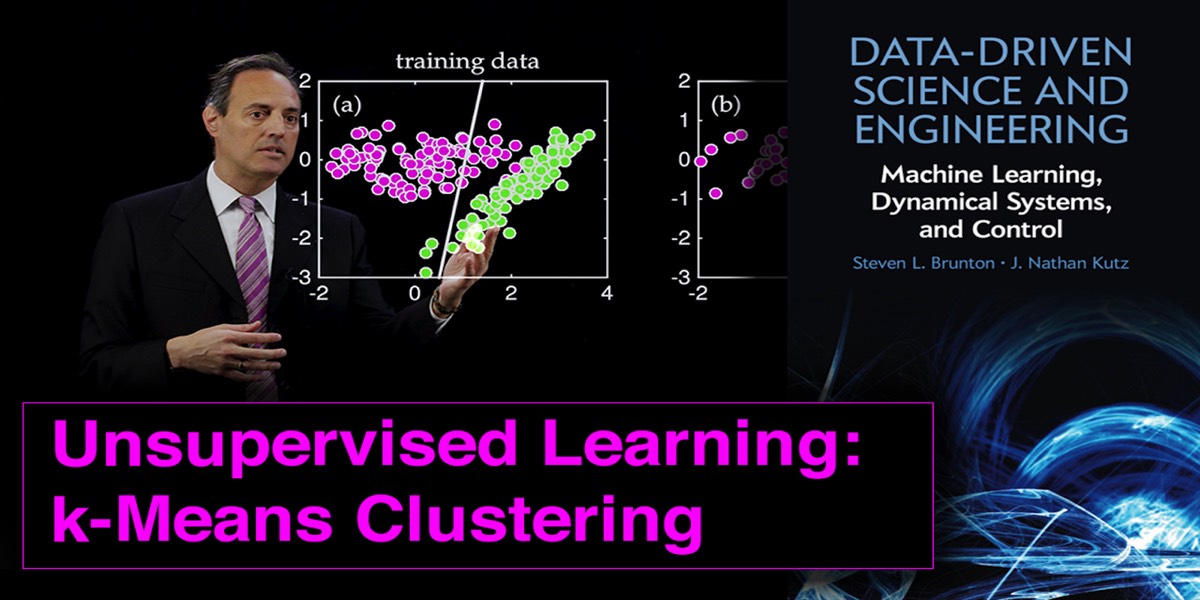
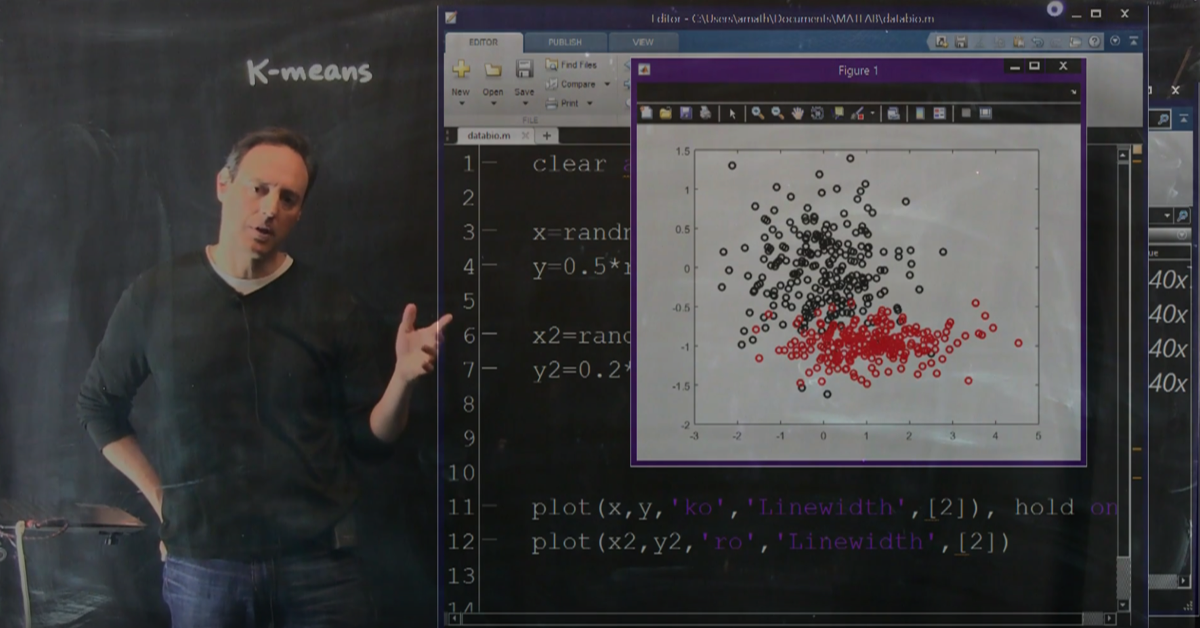
The goal of data mining and machine learning is to construct and exploit the intrinsic low-rank feature space of a given data set. The feature space can be found in an unsupervised fashion by an algorithm, or it can be explicitly constructed by expert knowledge and/or correlations among the data. For eigenfaces, the features are the PCA modes generated by the SVD. Thus each PCA mode is high- dimensional, but the only quantity of importance in feature space is the weight of that particular mode in representing a given face. If one performs an r-rank truncation, then any face needs only r features to represent it in feature space. This ultimately gives a low-rank embedding of the data in an interpretable set of r features that can be leveraged for diagnostics, prediction, reconstruction and/or control.
The goal of data mining and machine learning is to construct and exploit the intrinsic low-rank feature space of a given data set. The feature space can be found in an unsupervised fashion by an algorithm, or it can be explicitly constructed by expert knowledge and/or correlations among the data. For eigenfaces, the features are the PCA modes generated by the SVD. Thus each PCA mode is high- dimensional, but the only quantity of importance in feature space is the weight of that particular mode in representing a given face. If one performs an r-rank truncation, then any face needs only r features to represent it in feature space. This ultimately gives a low-rank embedding of the data in an interpretable set of r features that can be leveraged for diagnostics, prediction, reconstruction and/or control.
Supplementary Videos